пятница, 8 апреля 2016 г.

Как крутить... - Зубастые планеты.

Честно говоря, говоря, что показать кручение шарикоподшипника было моей целью, я не совсем был честен. После того, как я без всякого напряжения закрутил одинокий шарик, мне сказали, что простой анимацией нельзя сделать не просто планетарный механизм, а именно  планетарный редуктор. Вряд ли кто-то будет спорить, что подшипник - это не совсем то же, что редуктор. Поэтому, как человек честный (пытаюсь по мере сил), я должен честно (по мере возможностей) сделать планетарный редуктор. И сделаю.

0. Delphi, File | New | Multi-Device Application, Blank Application. Сохраняем: модуль - 'uMain', проект - 'Planetary'.

Но! Для начала надо сказать, что редуктор - это куча зубов. А сколько их надо, какой ширины, глубины, формы? Я не знаток гипо-, эпи- циклоид и эвольвент, модулей зацепления зубчатого колеса и прочей сложной механики. Поэтому я просто из палитры Shapes взял TPath, посмотрел на картинку редуктора и изобразил нечто, похожее на зуб.



Зуб растёт вниз, т.к. я решил начать с венечной, коронной (или как её ещё там называют?) внешней зубчатой окружности, у которой зубы смотрят во внутрь. Сначала я сделал простой треугольник. Но потом решил, что это будет уж совсем неинтересно, и использовал вместо прямых линий две кривые Безье: TPаth.Data = 'M0,0 C0.25,0.5 0,0.25 0.5,1 C1,0.25 0.75,0.5 1,0'.  Вот с этим зубом, подобно воссоздающему скелет динозавра по одной найденной кости палеонтологу, я и построю свою машину.

1. Привычно бросаю на форму TLayout  (Align = Center, Size = 350x350) и на него ещё один TLayout (Align = Top). Вот тут придётся задуматься - сколько делать зубов и какого размера, чтобы они могли все уместиться на окружности. 

На настоящем редукторе (не знаю от чего он) я насчитал 35 зубов. У меня для ровного счёта пусть будет 36 - по 1 на 10º окружности. Тогда для диаметра 350 ширина зуба: 350*π/36 ≈ 30. Прикинув, что если оставить высоту TPath по-умолчанию 50 и дать такой же высоты зубы сателлитам и центральному валу, то в механизме уж очень мало место для движения получается, я решил сократить размер зуба по высоте в два раза. Мне показалось, что отнимать по 25 с двух сторон даже как-то удобнее, чем, скажем, 30. 

Итак, установив Layout2.Height = 25, бросаем на Layout2 новенький TPath (Data = 'M0,0 C0.25,0.5 0,0.25 0.5,1 C1,0.25 0.75,0.5 1,0', Align = Center, Width = 30, Height = 25,  RotationCenter.Y = 7). 7 - это 350/2/25, где 350 - диаметр окружности, а 25 - высота зуба. Оказалось, что высота в 25 - это действительно очень удобная высота.

Потом я скопировал зуб 8 раз - получилось 9 зубов. А потом я взял все эти зубы и сделал ещё 3 копии - вот и вышло 36 штук. Теперь - только пробежаться и расставить RotationAngle = 10, 20..360. Оказывается, это совсем не трудно.


2. Пришла пора подумать о шестерёнках-звёздочках-планетах-спутниках. Для начала я скопировал  сделанный уже круг зубов и повыдергивал из него каждый второй, а потом ещё раз каждый второй. Осталось 9. На самом деле не важно, как поступите вы, главное, чтобы RotationAngle = 0, 40, ..., 320. 

Прикинув диаметр внутренней окружности зубов (9*30/3 = 90, где 3 ≈ π) и внешний диаметр (90 + 2*25 = 140), я решил, что это слишком много - центральный вал (солнечная шестерня) будет слишком узким (350 - 2*140 = 70). Поэтому я уменьшил ширину зубов до 25. По предварительным прикидкам внешний диаметр сателлита должен быть 125 (≈ 25<в>*2+[25<ш>*9/3], где 25<в> - высота, а 25<ш> - ширина зуба), и RotationCenter.Y = 2,5 (125/2/25). Однако, я быстро убедился, что квадратики 25х25, размещённые на окружности ø75, не соприкасаются углами. Поэтому я уменьшил диаметр вписанной окружности до 60 - RotationCenter.Y = 2,2 ([25*2 + 60]/2/25). 

То, что получилось, ещё на звёздочку похоже не очень - зубы смотрят не в ту сторону. Это потому, что RotationCenter.Y находится ниже корпуса фигуры. Если мы поместим его выше, то тогда зубы закрутятся не вниз, а вверх, образуя нормальное зубчатое колесо. Для этого RotationCenter.Y должен быть отрицательным. Надо только понимать, что при этом позиция фигуры будет на целый корпус ближе к центру вращения. Поэтому просто поменять знак - недостаточно, надо RotationCenter.Y ещё и уменьшить на 1 по модулю: -1,2. Можно отметить зубы  в Structure и поменять свойство у всех разом. А чтобы оставить звёздочку внутри большого кольца, изменим Layout4.Align с Top на Bottom. 


Невозможно не заметить, что при таком расположении зубов наша шестерня должна быть прижата к верхнему краю. Поэтому на Layout3 кладём новый TLayout (Align = Top, Height = 110 - высота звезды). Но перетаскивать на новенького Layout4 не спешим. Надо предусмотреть ещё, что нам понадобятся одно вращение вокруг общего центра для создания клонов и другое вращение вокруг собственной оси для анимации. Поэтому на Layout5 добавляем Layout6 (Align = HorzCenter), а на него - Layout7 (Align = Client), а уже на Layout7 перетаскиваем Layout4.

Но что же получилось? Зубцы вгрызаются друг в друга! Опустим звёздочку на 10 единиц ниже, установив размер Layout3 в 330х330. И давайте заполним зияющую пустоту, поместив на  Layout7 окружность (Align = Center, Size = 60x60). Чтобы окружность не съезжала, добавим на Layout4 уравновешивающий TLayout (Align = Top, Height = 25). Для получения монолитности звезды щёлкаем на окружности правой кнопкой мыши и выбираем Control|Send to Back. Если результата сразу не видно, пощёлкайте вокруг - всё обязательно станет на свои места.

Итак, можно уже устанавливать вращение. Для Layout3.RotationAngle выбираем Create New TFloatAnimation, Duration = 36 (по секунде на зуб), Enabled = True, Loop = True, StopValue = 360. Для Layout7.RotationAngle тоже выбираем Create New TFloatAnimation, Duration = 9 (по секунде на зуб), Enabled = True, (внимание!) Inverse = True, Loop = True, StopValue = 360. Посмотрим, что получилось.


Запустив полученное приложение, можно увидеть, что сначала звёздочка крутится вполне реалистично. Но уже начиная где-то с 3-го круга, она заметно начинает отставать в собственном вращении, и её зубцы начинают всё больше и больше накладываться на зубцы коронного колеса, что, разумеется, сильно портит впечатление от проделанной нами работы.

Очевидно, что между двумя TAnimation накапливается погрешность расчётов. Если с гладкими шариками такие рассогласования сильно в глаза не бросаются, то при анимации зубчатых передач такого рода "скольжения" не заметить уже невозможно. Что же делать? Выходит, что вся затея изначально была обречена на неудачу?

Не будем отчаиваться! Давайте просто выравняем раскадровку анимаций, установив им одинаковую продолжительность действия. Сделаем FloatAnimation2.Duration = 36, как у FloatAnimation1. А чтобы увеличенное время не пропадало зря, увеличим соответственно и угол поворота - StopValue = 1440 вместо прежних 360. Таким образом мы не только согласовали орбитальное и собственное вращения шестерни, но и получили удобный способ изменять общий период вращения - достаточно перейти в тестовое представление дизайнера и поиском и заменой пройтись по всем Duration, сколько бы их ни было.

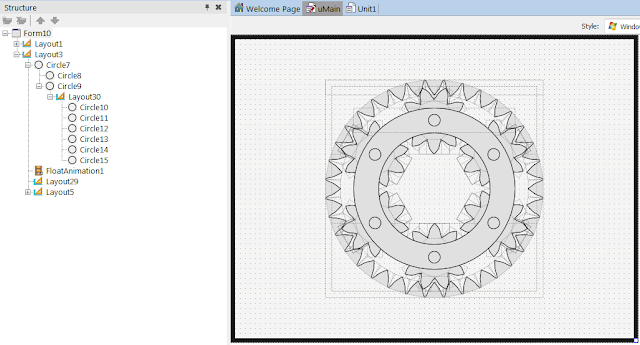
3. Размножим орбитальную группировку. Мне не приходилось видеть редукторы с одним сателлитом, обычно - с тремя или четырьмя. Но, как говорится, стрелять - так стрелять! Сделаем сразу полдюжины.

Установим Layout6.RotationCenter.Y = 1,5 (330/2/110, где 330 - высота большого Layout3, 110 -  высота самого Layout6). После этого сделаем копии Layout6 внутри Layout5, чтобы всего было 6 звёзд. Теперь бегаем по RotationAngle и расставляем 60, 120, ..., 300.

Шестёрка шестерёнок получилась плотной, но в этом нет ничего страшного. Легко можно посчитать, что радиус проходящей через центры звёздочек окружности - 110. Поскольку вершины правильного шестиугольника находятся друг от друга на расстоянии радиуса описывающей окружности, наши звёздочки располагаются как раз так, что их собственные описывающие внешние окружности попарно соприкасаются в одной общей точке. Можно было бы даже подумать, что при вращении звёздочки будут чиркать друг о друга кончиками зубьев. Но этого не случится, т.к. количество зубцов у них - нечётное, т.е. напротив каждого зубца как раз находится вырез у соседней звёздочки. Здорово я угадал с размерами?

Наложим на сателлиты водило. Делаем почти так же, как делали сепаратор подшипника. Сначала на Layout3, чтобы компенсировать смещение центра из-за верхнего Layout5, бросаем  новый соразмерный TLayout, прижав его к низу (Align = Bottom, Height = 110). Потом на Layout3 кладём кружок - (Align = Center, Fill.Kind = None, Stroke.Color = #FFE0E0E0 - скопировали из заливки, Stroke.Thickness = 40, Size = 260x260). На этот Circle7 кидаем Circle8 (Align = Center, Fill.Kind = None, Size = 180x180) и потом также на Circle7 добавляем Circle9 (Fill.Kind = None, Align = Client).

Получившееся кольцо остро нуждается в украшениях. Добавим торцы осей сателлитов. На Circle9 кладём TLayout (Align = Top, Height = 40), на него - Circle10 (Align = Center, Size = 20x20, RotationCenter.Y = 6). Размножаем Circle10 до 6 штук и ставим кружкам RotationAngle = 60, ..., 300. Так всё планеты встали на свою орбиту и никуда с неё уже не денутся.


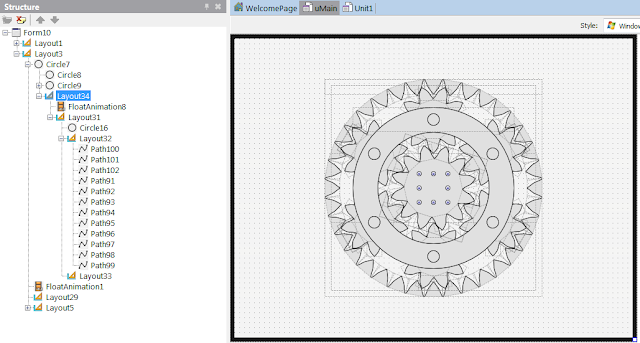
4. Приступим к центру. Новое зубчатое колесо - новые расчёты. Сколько сделать зубцов для солнечной шестерни? Кажется, что между внутренними зубцами планет мы можем воткнуть по два. Стало быть, всего 12. А с каким диаметром? Для примера, зубцы коронной передачи имеют внутреннюю окружность с радиусом 300 (350 - 25*2), а внешняя окружность сателлитов - 330, т.е. на 30 больше. Значит, если внутренний диаметр сателлитов 110, то размер солнечной шестерни должен быть 140. Начнём?

Возьмём уже готовую шестерню - Layout7, скопируем её на форму. Получилось не очень здорово, но мы не привыкли отступать: Layout7.Align = Center, Size = 140x140. Уже лучше, но надо продолжать. Возьмём 3 любых PathXX на Layout32, и сделаем их копии рядом. Потом отметим в Structure все 12  зубцов (или зубов? зубьев?), сделаем им всем RotationCenter.Y = -1,8 (1 - 140/2/25) и пойдём расставлять каждому по отдельности RotationAngle = 30, 60, ..., 330.

Однако, получилось, что зубцы колёс пересекаются. Давайте, повернём Layout31.RotationAngle на 15... нет, лучше на 17,5 градусов. И да, заполняющую окружность увеличим до 100х100... нет, лучше до 96.

Разберёмся с унаследованной анимацией. Она теперь не инверсная (Inverse = False) и за указанный период должна делать не 4 (36/9) оборота, а только 3 (36/12), т.е. StopValue = 1080. Однако, очень важно отметить, что беря для вращения соотношение 9/12 между солнцем и планетами мы не учитывали, что это всё движется внутри короны. Чтобы это учесть, математикой заниматься не будем, а просто перетащим Layout31 куда-нибудь на Circle7. Всё?

Нет, запуск показывает неприглядную картину - солнце дёргается, отстаёт. И не помогает даже FloatAnimation8.StartFromCurrent = True! Что делать? На Circle7 добавим Layout34 (Align = Center), а уже на него перетащим Layout31. FloatAnimation8 же спустим с Layout31 на Layout34. StartFromCurrent можно выключить. Вот теперь - всё!


Заключение.
Не успели мы сосчитать до пяти, как у нас уже есть чудный планетарный редуктор. Даже без программирования. И если какой-нибудь кандидат технических наук, защитивший диссертацию на системах автоматизированного проектирования, и теперь станет утверждать, что для этого обязательно нужны синусы и косинусы, просто обсудите с ним эту картинку.

Кстати, я заметил, что изобретённый мной зуб механической передачи трётся о своих соседей просто страшным образом. Он явно не заточен по эвольвенте. Если вы можете улучшить конструкцию, добро пожаловать: https://github.com/alhymov/Planetary.git

Возможно, продолжение следует...

Автор: на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)